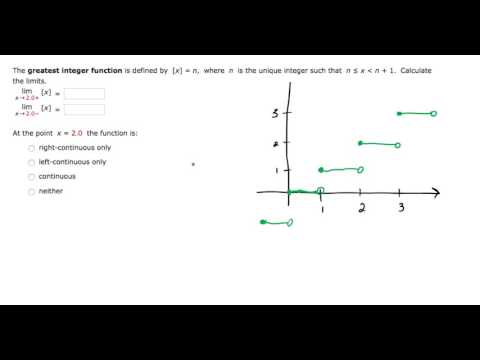
Points Of Continuity For The Floor Function

Discontinuity at a point the definition for continuity at a point may make more sense as you see it applied to functions with discontinuities.

Points of continuity for the floor function. At points of continuity the series converges to the true. A real function that is a function from real numbers to real numbers can be represented by a graph in the cartesian plane. For example the floor function has jump discontinuities at the integers. Continuous functions are of utmost importance in mathematics functions and applications however not all functions are continuous.

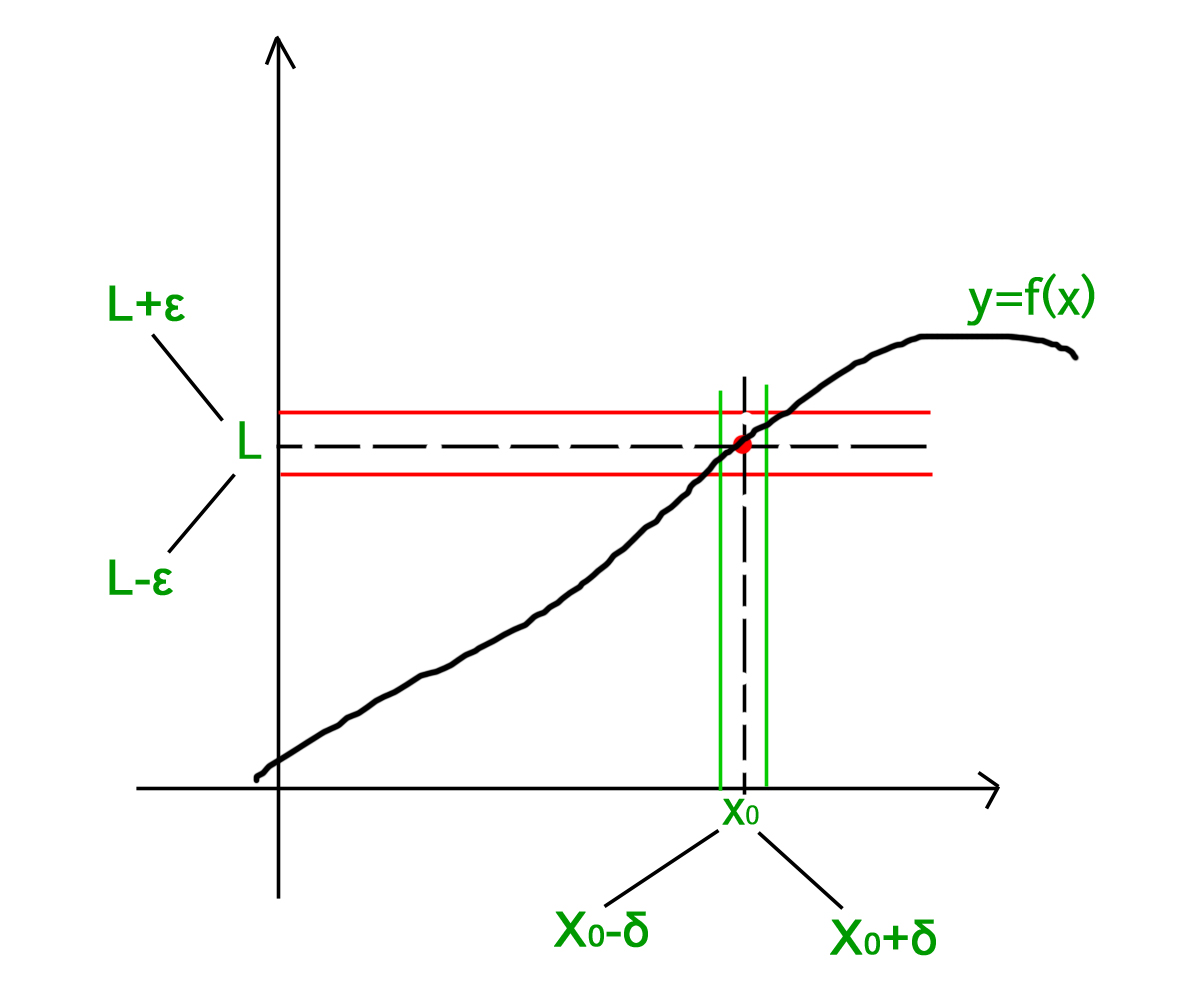
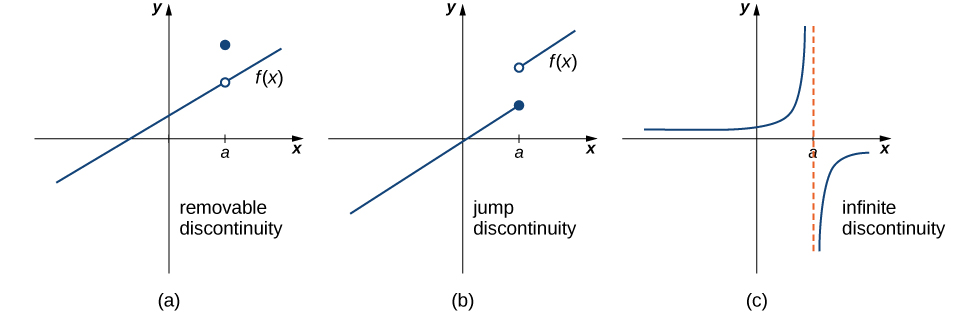
A function f x is continuous at a point where x c if exists f c exists that is c is in the domain of f a function is continuous on an interval if it is continuous at every point in the interval. A real valued univariate function has a jump discontinuity at a point in its domain provided that and both exist are finite and that. A more mathematically rigorous definition is given below. Such a function is continuous if roughly speaking the graph is a single unbroken curve whose domain is the entire real line.

A rigorous definition of continuity of real functions is usually given in a first. At it jumps from the limit approaching from the left to the limit approaching from the right. A function is continuous if and only. If a function is not continuous at a point in its domain one says that it has a discontinuity there.

In mathematical analysis semi continuity or semicontinuity is a property of extended real valued functions that is weaker than continuity an extended real valued function f is upper respectively lower semi continuous at a point x 0 if roughly speaking the function values for arguments near x 0 are not much higher respectively lower than f x 0. A third type is an infinite. For y fixed and x a multiple of y the fourier series given converges to y 2 rather than to x mod y 0.